SGD Optimizers

Basics

字数统计: 687阅读时长: 3 min

 2020/05/20   Share

Materials

survey paper of the gradient descent methods

Basic Gradient Descent

从batch大小的角度来看，GD方法可以分为以下三类：

Batch Gradient Descent: 整个数据集都参与gradient的计算
Stochastic Gradient Descent: 每次计算gradient时都只从数据集中sample 1个data
Mini-batch Stochastic Gradient Descent: 每次sample一个小的batch进行gradient计算

通常意义上我们说的SGD都指的是mini-batch SGD. 如下式，其中 $\eta$ 表示学习率

$\theta=\theta-\eta \cdot \nabla_{\theta} J(\theta)$

Momentum

Momentum想要避免前后两个time step之间太过于剧烈的gradient变动，采用了CS中常见的平滑策略。以下的示例展示了这种平滑策略：假设a是不断在0, 1之间震荡的gradient，那么变量b采取以下等式

$b_t=\alpha b_{t-1}+(1-\alpha)a_t$

则得到以下经过平滑后的曲线效果

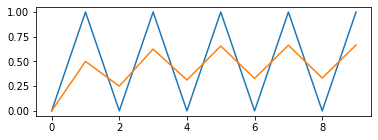
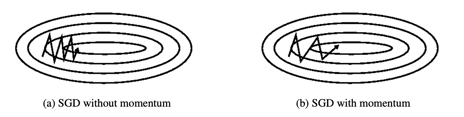
从而给出了平滑gradient的momentum.

$\begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta) \\ \theta &=\theta-v_{t} \end{aligned}$

Adagrad

Adagrad希望能够做到对于每个参数的更新都能够做到自适应，而不是统一使用一个学习率$\eta$. 在第$t+1$个时间步第$i$个参数$\theta_{t,i}$的更新法则为

$\theta_{t+1, i}=\theta_{t, i}-\frac{\eta}{\sqrt{G_{t, i i}+\epsilon}} \cdot g_{t, i}$

其中参数更新自适应的scale $G_{t,ii}$ 表示的是该参数在之前时间步对应gradient的平方和

$G_{t, i i}=\sum_{\tau=1}^{t} g_{\tau, i}^{2}$

向量化后得到

$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{G_{t}+\epsilon}} \odot g_{t}$

Adadelta

Adagrad的最大问题就在于learning rate随着time step的增加不可避免地diminish. 为了缓解这个问题，Adadelta保持了一个记录过去gradient的窗口。但是在内存中显式地保存过去$w$个gradient矩阵并不是特别理想的操作，为此Adadelta采用了类似于Momentum的平滑方法

$E\left[g^{2}\right]_{t}=\rho E\left[g^{2}\right]_{t-1}+(1-\rho) g_{t}^{2}$

取$\rho=0.5$同时再求根就得到了RMS(均方根)，则得到了RMSprop方法

$E\left[g^{2}\right]_{t}=0.9 E\left[g^{2}\right]_{t-1}+0.1 g_{t}^{2}$

Adam

Adam同时想要达到Adaptive Learning Rate和Momentum的平滑化。首先定义gradient的两阶的近似,

$\begin{aligned} m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\ v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \end{aligned}$

接着为了纠正这两个近似的bias,

$\begin{aligned} \hat{m}_{t} &=\frac{m_{t}}{1-\beta_{1}^{t}} \\ \hat{v}_{t} &=\frac{v_{t}}{1-\beta_{2}^{t}} \end{aligned}$

最终的参数更新按照以下

$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} \hat{m}_{t}$