Information Competing Process for Learning Diversified Representations

字数统计: 761阅读时长: 4 min

 2020/05/27   Share

Materials

NIPs-2019 paper “Information Competing Process for Learning Diversified Representations”

Motivation

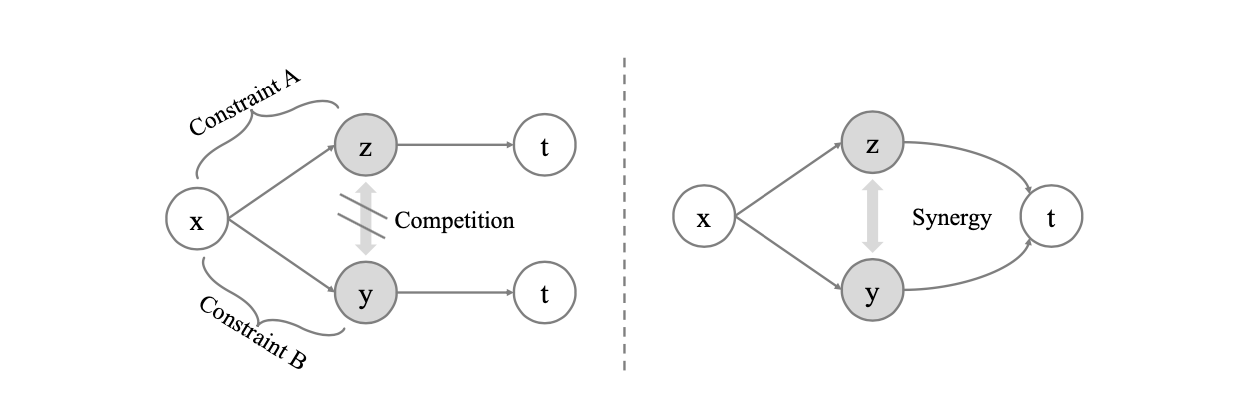
Aiming to enrich the information carried by feature representations, ICP separates a representation into two parts with different mutual information constraints. The separated parts are forced to accomplish the downstream task independently in a competitive environment which prevents the two parts from learning what each other learned for the downstream task. Such competing parts are then combined synergistically to complete the task.

Representation Collaboration

The Competitive Collaboration method is the most relevant to our work. It defines a three-player game with two competitors and a moderator, where the moderator takes the role of a critic and the two competitors collaborate to train the moderator. Unlike Competitive Collaboration, the proposed ICP enforces two (or more) representation parts to be complementary through different mutual information constraints for the same downstream task by a competitive environment, which endows the capability of learning more discriminative and disentangled representations.

Methods

Objectives

首先将supervised和self-supervised两个setting中的objective进行一下统一. In supervised setting, $t$ represents the label of input $xt$. In self-supervised setting, $xt$ represents the input $tx$ itself. This leads to the unified objective function linking the representation $rx$ of input $x$ and target $t$ as:

$\max \mathcal I(r,t)$

Seperating Representations

Directly separate the representation $r$ into two parts $[z, y]$. Specifically, we constrain the information capacity of representation part $z$ while increasing the information capacity of representation part $y$.

$\max [\mathcal{I}(r, t)+\alpha \mathcal{I}(y, x)-\beta \mathcal{I}(z, x)]$

Representation Competition

ICP prevents $z$ and $y$ from knowing what each other learned for the downstream task, which is realized by enforcing $z$ and $y$ independent of each other.

$\max [\mathcal{I}(r, t)+\alpha \mathcal{I}(y, x)-\beta \mathcal{I}(z, x)+\mathcal{I}(z, t)+\mathcal{I}(y, t)-\gamma \mathcal{I}(z, y)]$

在形式上和我们想要做的InfoBal非常接近，我们将以上式子带入unsupervised learning的情境下，也就是target $t$ = input $x$:

$\begin{align} &\max [\mathcal{I}(r, t)+\alpha \mathcal{I}(y, x)-\beta \mathcal{I}(z, x)+\mathcal{I}(z, t)+\mathcal{I}(y, t)-\gamma \mathcal{I}(z, y)] \\ \Leftrightarrow& \max [\mathcal{I}(r, x)+\alpha \mathcal{I}(y, x)-\beta \mathcal{I}(z, x)+\mathcal{I}(z, x)+\mathcal{I}(y,x)-\gamma \mathcal{I}(z, y)] \\ \Leftrightarrow& \max [\mathcal{I}(r, x)+(\alpha+1) \mathcal{I}(y, x)+(1-\beta) \mathcal{I}(z, x)-\gamma \mathcal{I}(z, y)] \\ \Leftrightarrow& \max [\mathcal{I}(r, x)+\alpha^\prime \mathcal{I}(y, x)+\beta^\prime \mathcal{I}(z, x)-\gamma \mathcal{I}(z, y)] \\ \end{align}$

where $\alpha^\prime > 1$ and $\beta^\prime < 1$. 如果把$z$和$y$分别看作数据的两个view，那么中间两项就代表不同view和$X$ 之间的相关度；第一项代表全局representation和input之间的相关度；而最后一项就是view之间的InfoMin项。

Minimizing MI

本文采用的最小化MI的方法来源于variational inference. 同Maximizing MI的方法类似的，因为是为了最小化，所以我们希望能够找到$I(x,z)$的upper bound，然后直接去最小化这个upper bound. 首先我们有：

$\begin{align} \mathcal{I}(z, x) &=\iint P(z, x) \log \frac{P(z, x)}{P(z) P(x)} d x d z \\ &= \iint P(z, x) \log P(z | x) d x d z-\int P(z) \log P(z) d z \end{align}$

Let $Q(z)$ be a variational approximation of $P(z)$, we have:

$K L[P(z) \| Q(z)] \geq 0 \Rightarrow \int P(z) \log P(z) d z \geq \int P(z) \log Q(z) d z$

将该不等式带入MI的定义式，我们得到了一个tractable upper bound (why???).

$\mathcal{I}(z, x) \leq \iint P(z | x) P(x) \log \frac{P(z | x)}{Q(x)} d x d z=\mathbb{E}_{x \sim P(x)}[K L[P(z | x) \| Q(z)]]$

which enforces the extracted $z$ conditioned on $x$ to a predefined distribution $Q(z)$ such as a standard Gaussian distribution.

原文作者：Haizhou Shi

原文链接：http://www.shihaizhou.com/2020/05/27/Information-Competing-Process-for-Learning-Diversified-Representations/

发表日期：May 27th 2020, 2:57:20 pm

更新日期：May 28th 2020, 10:17:06 am