Materials
- CMU tutorial on Legendre transform
- Youtube short explanation on Legendre transform
- http://www.onmyphd.com/?p=legendre.fenchel.transform
Legendre Transform
Information in Functions
函数的本质是映射,映射包含了信息,那么如何衡量一个函数包含的信息量?对于离散函数,一种想法是在值域上计算信息熵通过衡量值域上分布的混乱度来进行估算,但这并没有包含关于这个函数的所有信息:定义域信息、N-阶导函数信息都被丢失了。同时下面的一个简单函数我们就已经很难找到一种quantify它所包含的信息:
计算函数包含的绝对信息也许不可行,但是受到可数集上定义”size”方法的启发,我们或许可以找到一种定义两个函数包含信息量的相对关系。例如函数$y=f(x)$和它的inverse function $x=f^{-1}(y)$ 就应该包含有等量的 information,原因是它们在被表示成集合上的映射图时是完全一样的。
或许我们可以将一个函数transform成另一个函数而保持他们的信息不变,Legendre Transform就是在这个语境下的一种function transform方法。
Aim
现有一个函数 $\mathrm{y}: x \mapsto \mathrm{y}(x)$, 它包含了很多信息,例如对于每一个给定的 $x$ 对应的函数值 $y$. 同时它也包含了slope at any given $x$. Legendre Transform的目标是将原函数转换为一个关于slope $p$ 的函数,同时保证这两个函数是具有同样的信息的。定义:
Failed attempt. 一个非常直观的想法就是我们将 $x$ 用 $p$ 来表示,即 $x = \mathrm y ^{\prime -1}(p)$, 然后反向代回原来的函数 $\mathrm y$. 由此我们得到以下的transformed $\tilde{\mathrm y}$:
那么我们需要验证这个transform导致了一部分信息的丢失,最好的方法是通过counter example,对于函数:
根据上式我们计算出:
我们发现最终的表达式里关于 $x_0$ 的信息丢失了:对于由不同 $x_0$ 构成的函数集合,它们都transform到了同一个函数上。但是我们只需要
Definition
Definition (Legendre Transformation). Legendre Transformation from a function $\mathrm y(x)$ to a new function $\mathrm y^\star (p)$ is defined as follow, where $p=\mathrm y^\prime (x)$ and no information is lost iff function $\mathrm y$ is convex (or concave, which is omitted in this blog):
为什么函数需要是convex: 因为只有convex的函数才能够建立 $x$ 和 $p$ 的一一映射,这也是Legendre Transform的一大限制。同时需要注意的是 $p=\mathrm y^\prime (x)$ 不是先于这个定义的条件,而是通过解决这个关于 $x$ 的最大化问题得到的结果:关于 $x$ 求导并使其导数为0,得到:
所以以上定义式等价于以下去掉 $\sup$ 符号的式子(在网上更多见的版本):
Properties
Geometric interpretation
在空间上我们可以认为Legendre Transformation建立了某点 $x$ 对应斜率 $p$ 和该点tangent的截距之间的函数关系。具体证明非常简单,作图即可。以下是帮助理解的图例:
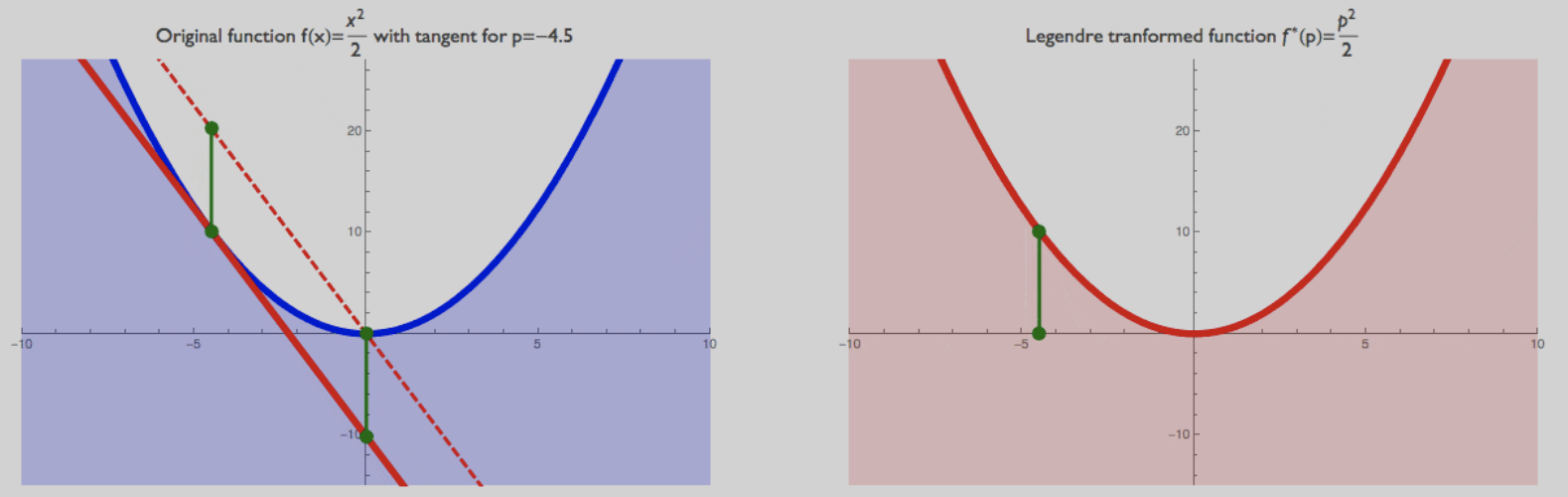
Inverse of derivatives
经过transform之后的函数 $\mathrm y^\star(p)$ 关于其自变量的导数和原函数有以下关系:
Inverse of Legendre Transformation
The Legendre Transformation of the Legendre Transformation of a function $\mathrm y$ is $\mathrm y$ itself, which is easy to prove.
同时因为这条式子,Legendre Transformation是一个不会导致函数信息损失的transformation.
Finding the min value
在一些情况下我们不方便直接去求原函数的最小值 $\mathrm y(x)_{min}$,但我们知道 $\mathrm y(x)$ 在取到极小值的时候一阶导数 $p=\mathrm y^\prime (x)=0$. 从而我们在知道了Legendre Transformation的情况下可以直接求极小值:
Fenchel Conjugate
寻找一个非凸函数的凸共轭的目标是:对于在(某个定义域内)任意斜率的直线,我们要找出这个使得该直线最靠近该非凸函数的截距值。如下图,对于给定斜率为 $s$ 的直线,我们想要找到截距 $b$ 使直线尽量靠近函数。最简单的想法是对所有 $x$ 求导,在导数等于零的点中找到一个最接近的直线。下图中,非常明显 $b_0$ 优于 $b_1$.
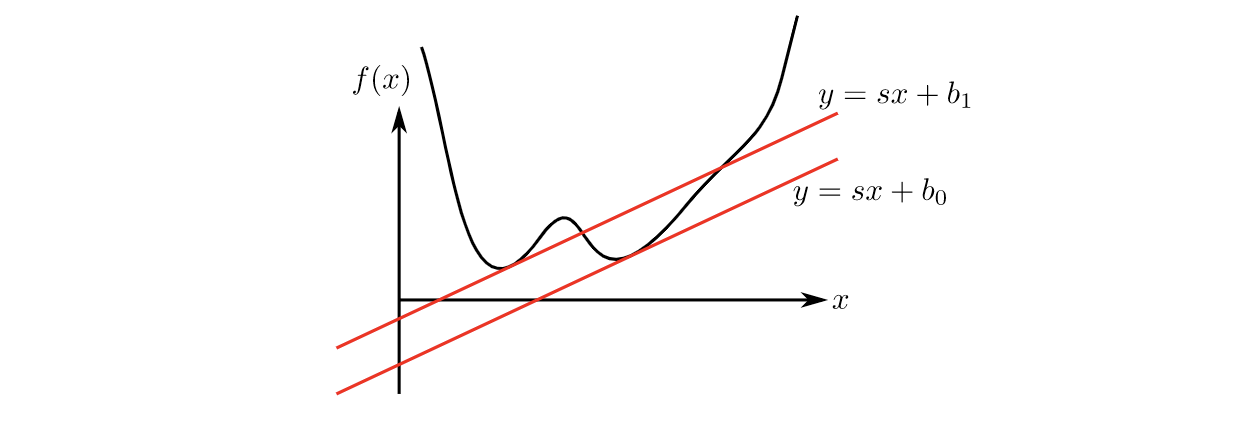
This more general rule applies to non-differentiable or non-convex functions. So, when a line with slope $\mathbf s$ crosses $f(\mathbf x)$, we have:
and we want the smallest value of $b$ for all $x$. Then:
所以从这里来看我们上面定义的Legendre Transform实际上是希望能够建立一个从slope到截距的映射,而这里我们的Fenchel Conjugate也是为了建立这样的映射:$f^{\star}(\mathbf{s})=-b$. 故而我们得到了Fenchel Conjugate的表示:
This is the Legendre-Fenchel transform, also known as convex conjugate. Note that now the transform is not reversible, i.e., you cannot get the original function by applying the transform to the transform. On the other hand, the transform of the transform is convex, even if the original function is not.