Tongzhou Wang, 2020 ICML的工作证明了,对于contrastive learning来说,alignment和uniformity的优化都是不能缺少的:仅有alignment约束而没有表征空间uniformity约束会导致representation collapse;而仅有uniformity又不会形成任何有意义的簇。从这个意义上讲,BYOL的成功无疑是令人困惑的。
观察BYOL的优化目标:
其中$q_w$是online network上多出来的predictor,我们将这个多出来的predictor显式地写出来是为了突出$q_w$是一个不能够被忽略的网络结构。在形式上,$\mathcal{L}_{\text{BYOL}}$和alignment都是MSE的loss,这个loss的作用是使两个网络的output最终能够吻合。因为EMA的效果是使target network在参数权重上直接靠近online,所以自然地,我们会考虑最终两个网络参数的convergence;而如果同时predictor $q_w$成为了一个identity mapping,那么$\mathcal{L}_{\text{BYOL}}$就完完全全退化成了alignment loss,随之而来的就是representation collapse。
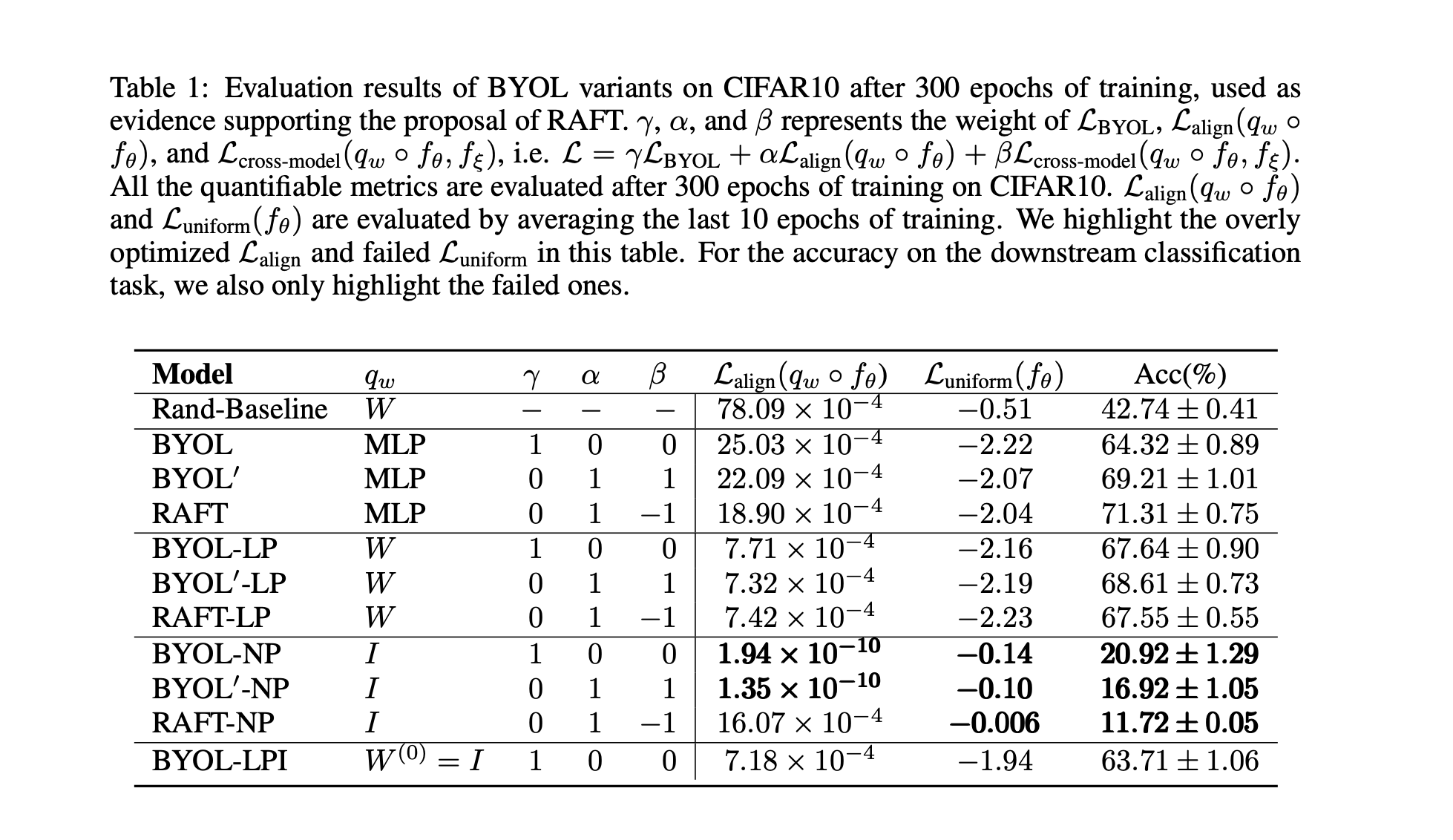
以上的推论过程是很有说服力的,因为这个退化解就在参数的可行域里,而要在理论上解释BYOL为什么不发生collapse就应该去说明BYOL如何防止参数坍缩到这个退化解。但BYOL的分析又有非常多的角度,因为它包含了太多的影响因素:data augmentation,EMA,BN,predictor等。根据已有的实验结果(最近BYOL原作者关于Batch Statistics的分析、原文章对EMA/predictor做的ablation),唯一影响BYOL是否collapse的因素只有predictor。我们的工作 Run Away From your Teacher: A New Self-Supervised Approach Solving the Puzzle of BYOL 部分解释了linear predictor在防止collapse方面的作用机理,以下是我们工作的介绍。
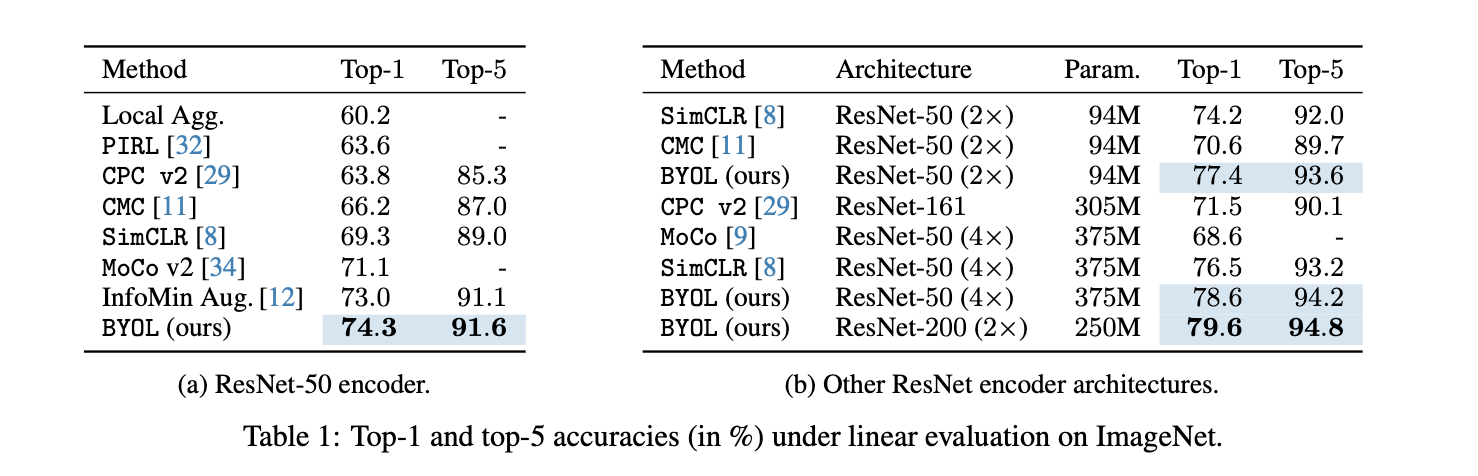
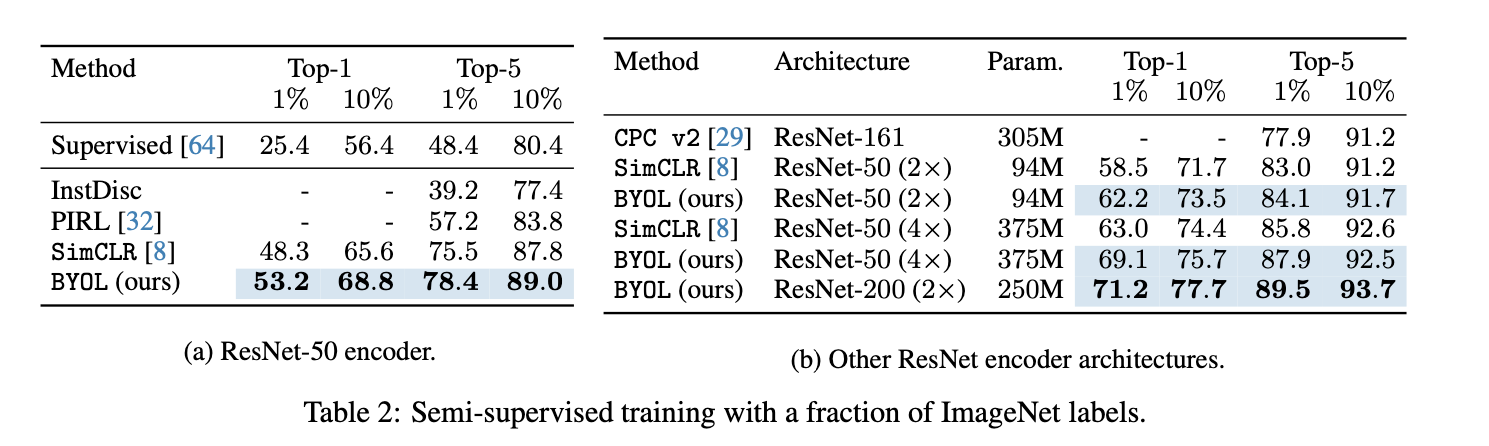
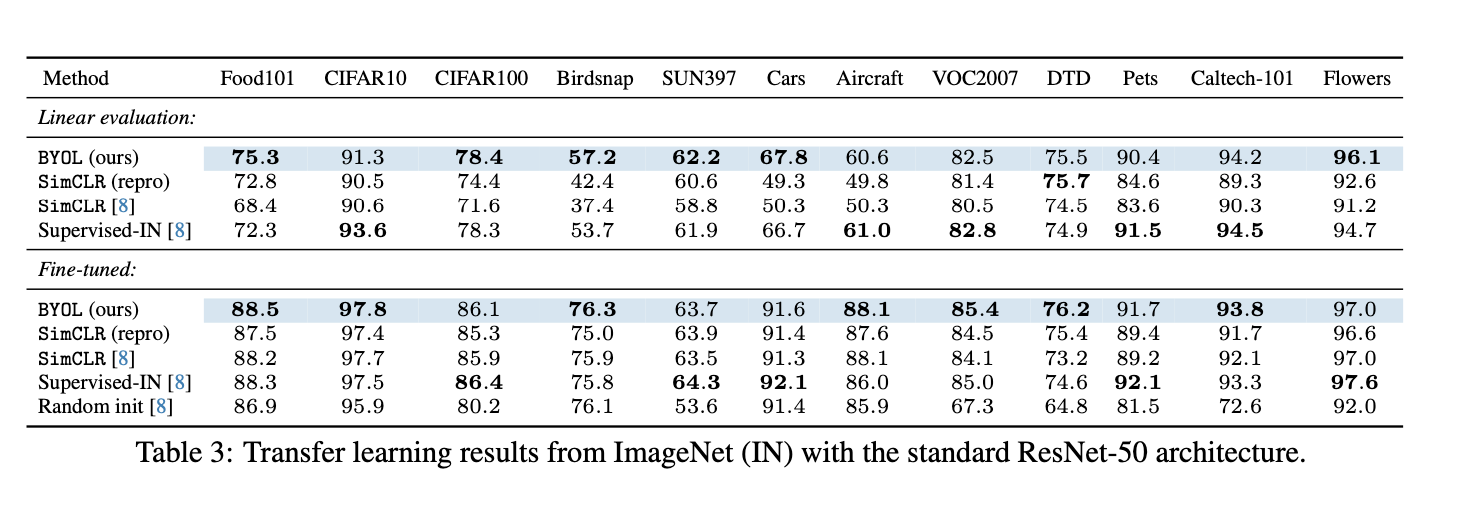
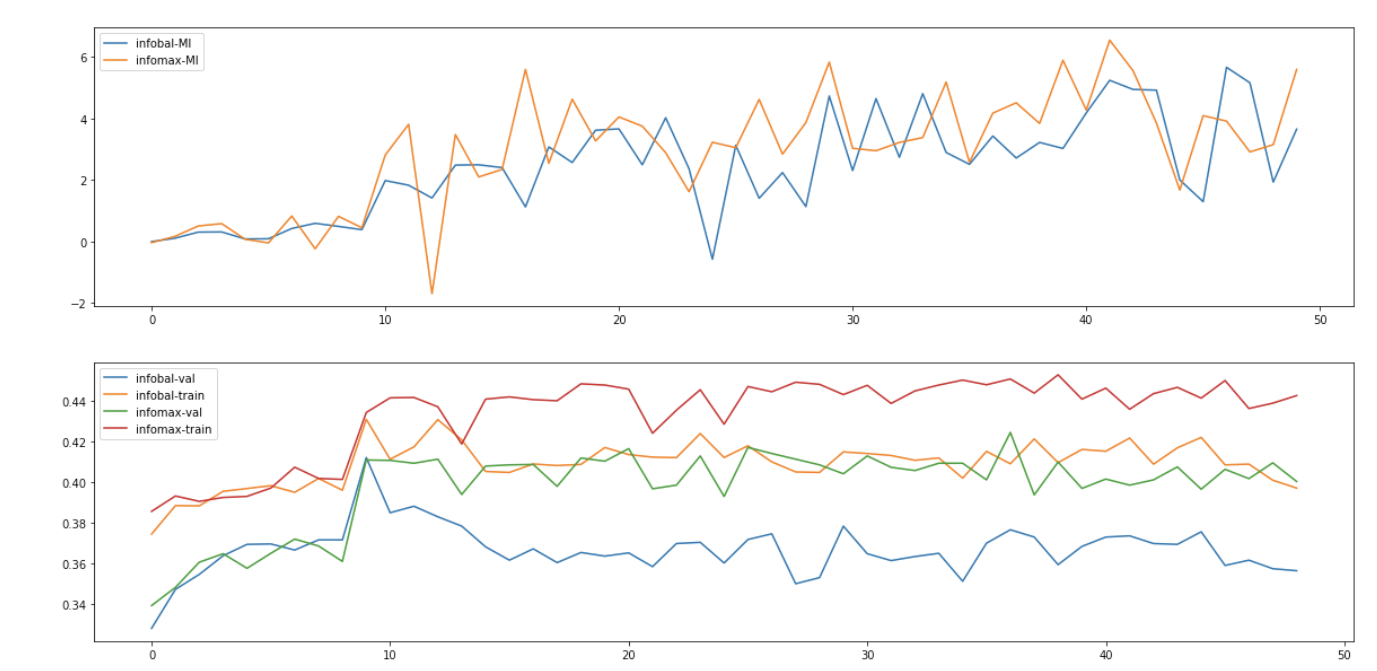
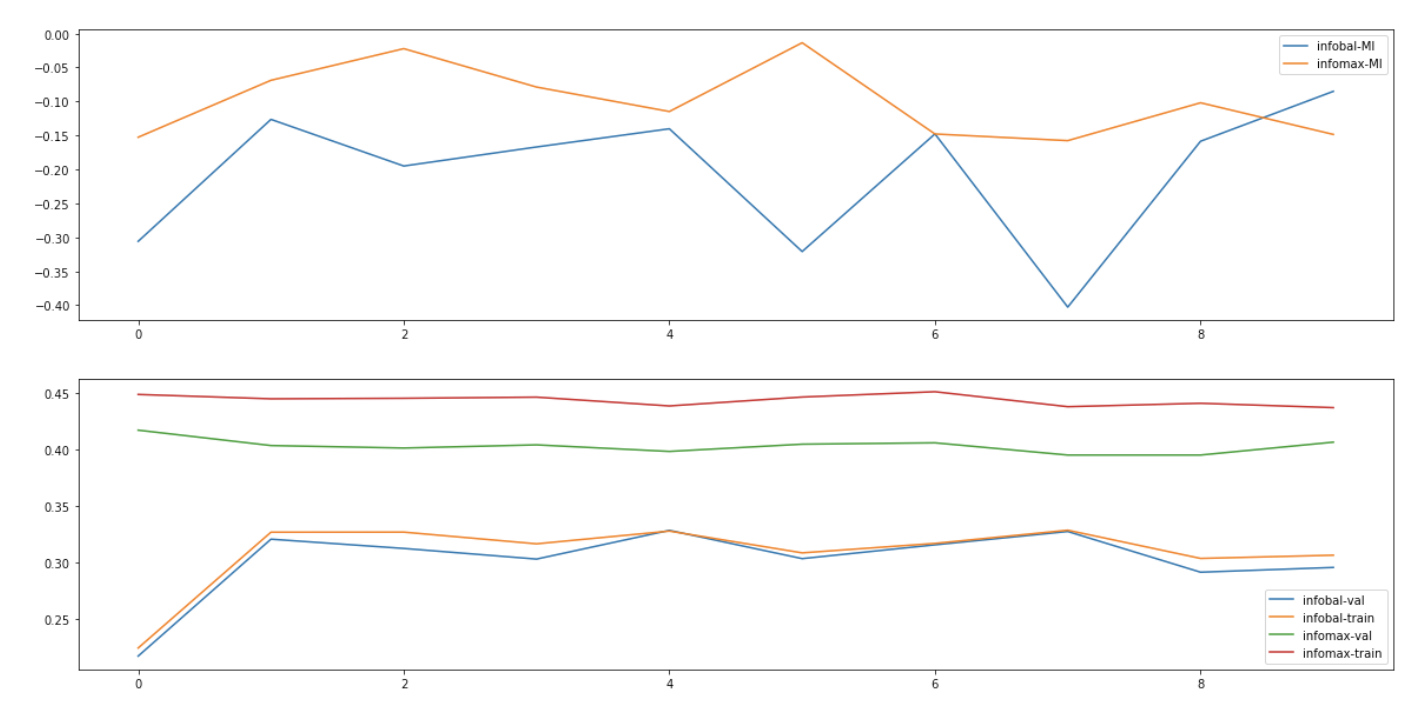
首先我们从实验上验证predictor对于防止collapse的重要性。通过替换不同的predictor类型(图中的MLPP/LP/LPI/NP 分别对应 MLP predictor/Linear predictor/Linear predictor initialized by $I$/No predictor),我们发现当没有predictor时BYOL的表现会下降到比random baseline更差,与之对应的是representation uniformity呈现负优化,也就说明了当缺少predictor的时候,BYOL会发生collapse。 另外值得注意的是当predictor为linear mapping的时候BYOL依然work,这为我们后面章节的分析提供了前提;甚至当我们显式地给predictor提供一个退化解($W=I$)作为初始化值时,BYOL依然work:在uniformity恶化了接近10个epoch之后它又奇迹般地复活了,并且在后续的训练中被不断优化,见下图(b)橙色曲线。
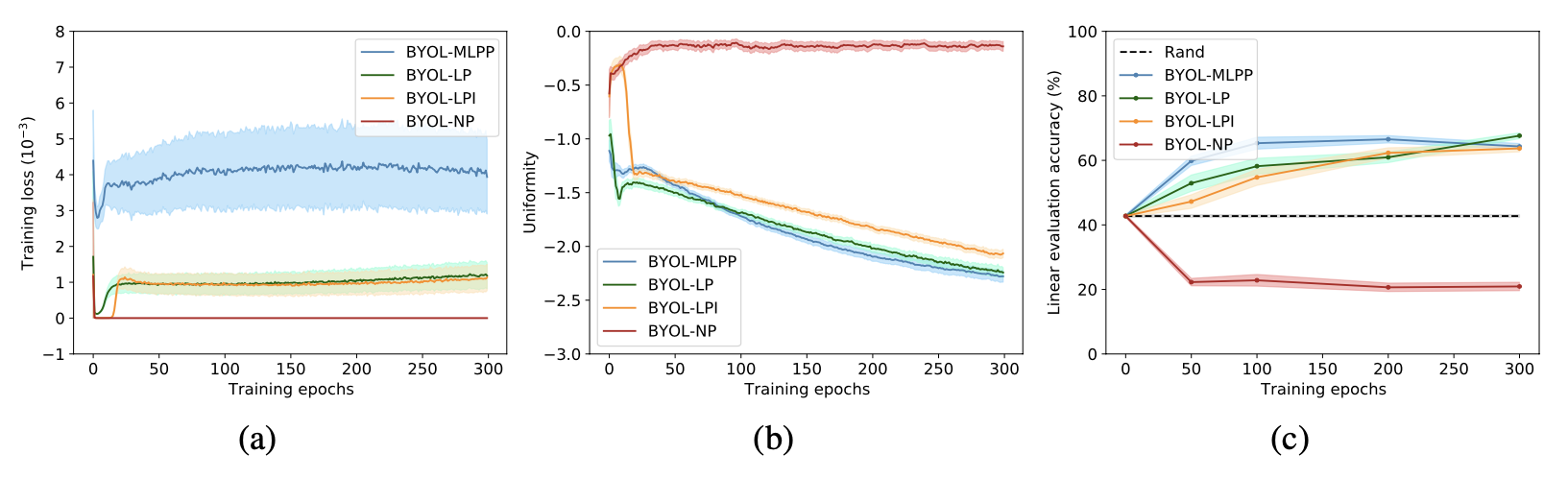
受到Tongzhou Wang, 2020 ICML工作启发,因为优化项$\mathcal{L}_{\text{BYOL}}$并不是严格的alignment loss,所以我们构造式地提取出alignment项。通过加减“同一个online network,不同的augmented view”项 $q_{w}\left(f_{\theta}\left(t_{2}(x)\right)\right)$,我们将$\mathcal{L}_{\text{BYOL}}$拆分成了三项:
推导过程中我们用 $x_i$ 来简记 $t_i(x)$.
这三项中的前两项非常容易解释:第一项是contrastive leanring中负责将同一个data的不同augmented view在representation space里align到一起的项,我们记为$\mathcal L_{\text{align}}$;第二项是online network去靠近自己历史版本的EMA,我们记为$\mathcal L_{\text{cross-model}}$;第三项作为交叉项则不太容易看出它的具体作用。在训练过程中我们estimate这三项分解出的loss,发现交叉项是唯一一个不降反升的指标。因此我们推测交叉项是一个不重要的loss,从而我们提出去优化$\mathcal{L}_{\text{BYOL}}$的上界$\mathcal{L}_{\text{BYOL}^\prime}$:
当$(\alpha, \beta)=(1,1)$时,就相当于将交叉项直接抹去,我们测试了该情况下的BYOL和BYOL$^\prime$在CIFAR10上的表现。我们发现这两者有线性predictor时,它们在alignment/uniformity/accuracy三个指标上都非常接近(下表LP部分)。这在经验上给我们将BYOL近似为BYOL$^\prime$提供了支持,但是理论上为什么交叉项可以省去,或者在什么条件下能够省去,我们没有在这篇工作中讨论,希望未来能够进一步研究。
现在我们转而研究BYOL$^\prime$为什么不会发生collapse。从形式上来看其实我们的任务并没有变得更加轻松:原先的$\mathcal{L}_{\text{BYOL}}$项是使得两个网络的output相互靠近,而现在的$\mathcal{L}_{\text{BYOL}^\prime}$包含了两项同样相互靠近的项$\mathcal{L}_{\text{align}}$和$\mathcal{L}_{\text{cross-model}}$,按照我们之前的推理,collapse依旧可能发生。注意到后一项的$\mathcal{L}_{\text{cross-model}}$是唯一能够使得表征空间的uniformity得到优化的动力,但是他们在形式上却完全不同:uniformity loss鼓励相互独立的样本在表征空间里拉开距离,而$\mathcal{L}_{\text{cross-model}}$却在鼓励拉近某种距离。
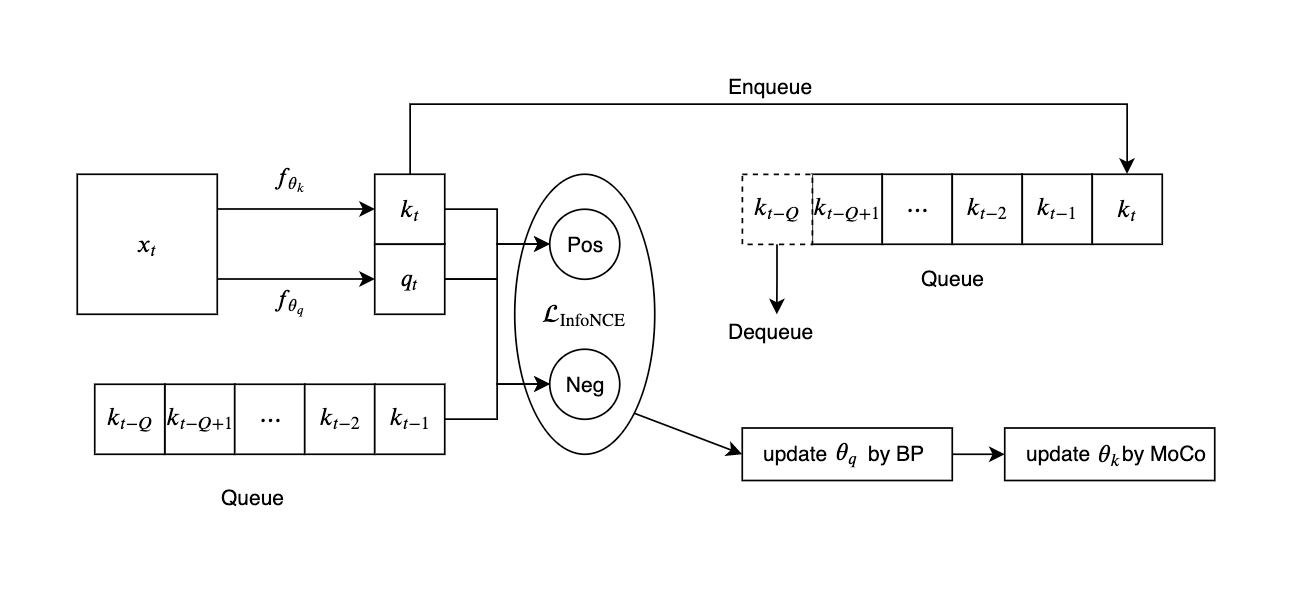
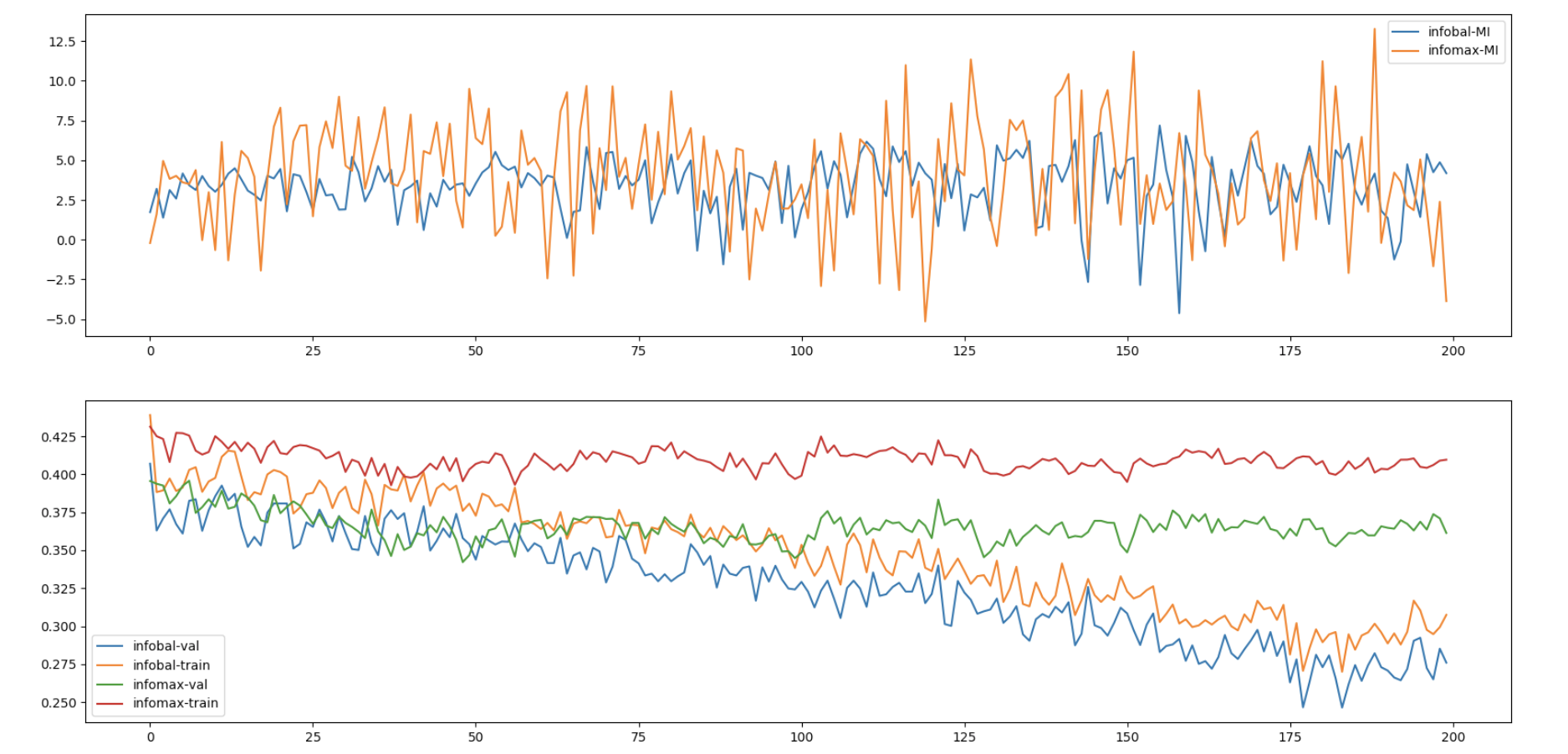
这里来到本篇工作最为重要的一部分:为了至少和uniformity loss的优化建立联系,我们尝试最大化$\mathcal{L}_{\text{cross-model}}$而不是最小化它,结果发现优化$\mathcal{L}_{\text{align}}-\mathcal{L}_{\text{cross-model}}$也依然是work的!据此(先抛开这个让人惊讶的现象为什么发生),我们提出了一个全新的自监督学习框架 Run Away From your Teacher (RAFT)。训练过程中,RAFT优化两个目标:拉近同一个data不同augmented view的representation,以及拉开和自己历史版本EMA(文章中称为Mean Teacher,MT)的距离。RAFT和BYOL框架的流程及优化目标见下图:
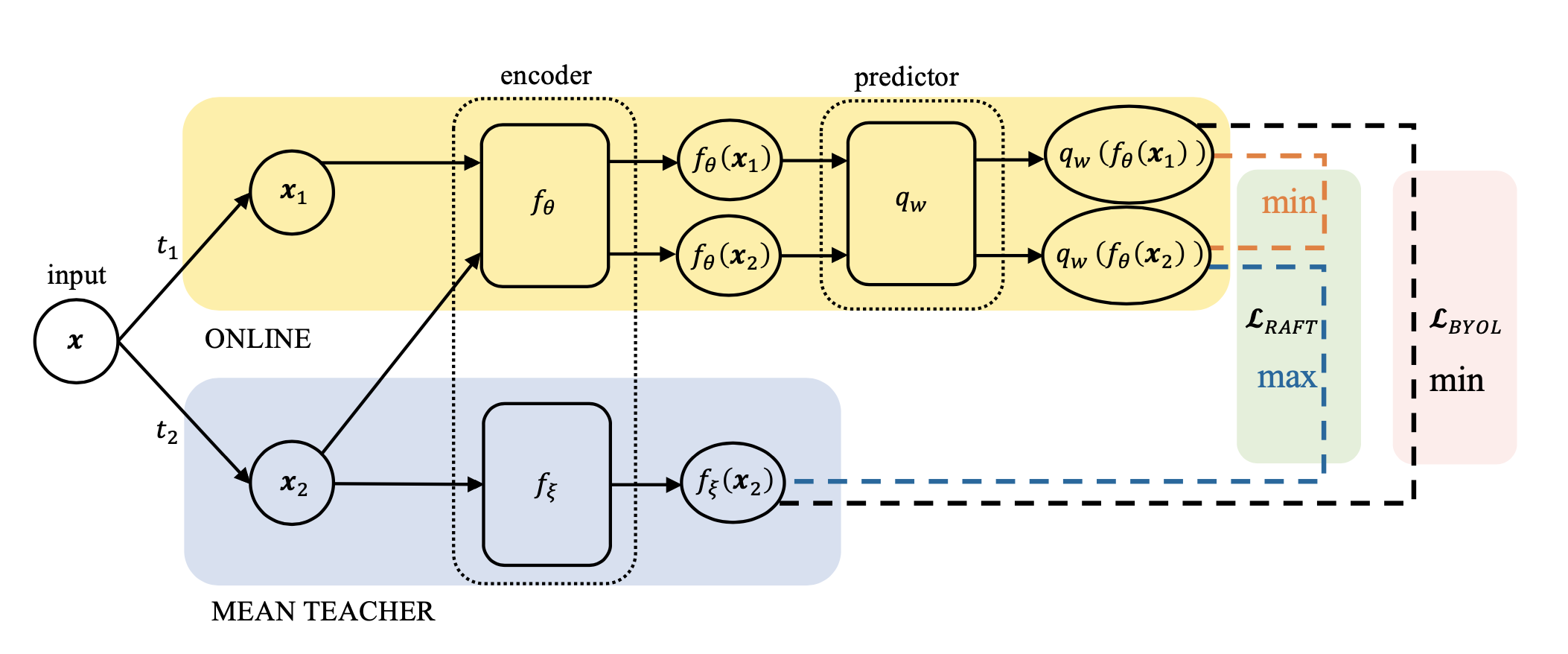
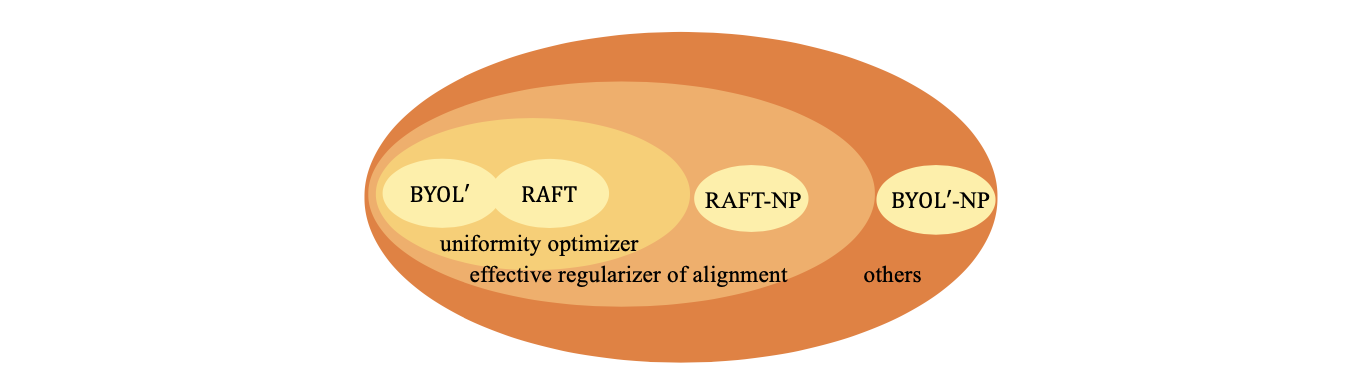
和BYOL相比,RAFT和BYOL$^\prime$的形式是disentangled,不同loss之间的权重也可以调节,因此更好;而RAFT和BYOL$^\prime$相比,RAFT中鼓励online远离MT的loss $-\mathcal{L}_{\text{cross-model}}$ 在去除掉predictor之后依旧是alignment loss的有效正则项,而当BYOL$^\prime$在去除predictor之后就失去了对alignment loss的约束(见前文的表中的NP部分)。从对alignment loss的正则效果来看,如下图所示,RAFT是相对于BYOL$^\prime$更为统一的方法,因此也更应该被作为MT的“正确”使用方法。其中值得探讨的问题是为什么RAFT在最后一层能够有效的正则alignment loss,但是却不能够防止中间表征层的collapse,这一疑问我们留给未来的工作。
RAFT避免的collapse的机制是直觉上成立的,如下图(b)所示。利用semi-supervised learning中Mean Teacher的部分结论:MT采用的model averaging可以被看成sample averaging的近似,我们发现如果MT给两个data representation的驱动力是相反的,那么这两个representation会在接下来的训练中持续远离对方,从而避免了collapse。
最后来看为什么RAFT能够帮助我们理解BYOL。我们发现当以下三个条件成立时:(1) 表征空间是一个超球面;(2) predictor为线性;(3) 球面表征空间上切向梯度被保留而径向梯度被舍弃,RAFT的训练轨迹和BYOL$^\prime$的训练轨迹存在一一映射关系。第一个条件是BYOL原paper的设置;第二个条件我们已经在之前经验性地说明了linear predictor不会导致collapse;第三个条件将梯度分解为切向和径向两个方向,由于表征空间是一个球面,所以样本点在表征空间中聚合和分散的驱动力(梯度)只有切向分量起作用。径向方向的梯度充其量只是一个scaler的作用,在学习率非常小的情况下可以忽略不计,因此第三个条件也是一个相对较弱的条件,在实际训练中非常容易可以做到。参考下图(a),假设除了优化目标不同之外其他所有的训练细节完全相同(包括模型架构、进入模型的数据顺序、优化器超参等等),BYOL$^\prime$中encoder network和predictor的参数分别用$(\theta, W)$表示并且初始化为$(\theta, W)=(\theta^{(0)}, W^{(0)})$,训练$N$个step得到的训练轨迹为$\{(\theta^{(k)}, W^{(k)})\}_{k=1}^N$,那么容易证明,初始化为$(\theta^\prime, W^\prime)=(\theta^{(0)}, -W^{(0)})$的RAFT算法得到的训练轨迹为$\{(\theta^{(k)}, -W^{(k)})\}_{k=1}^N$。这也就构造了一个任意setting下BYOL$^\prime$和RAFT的一一映射。
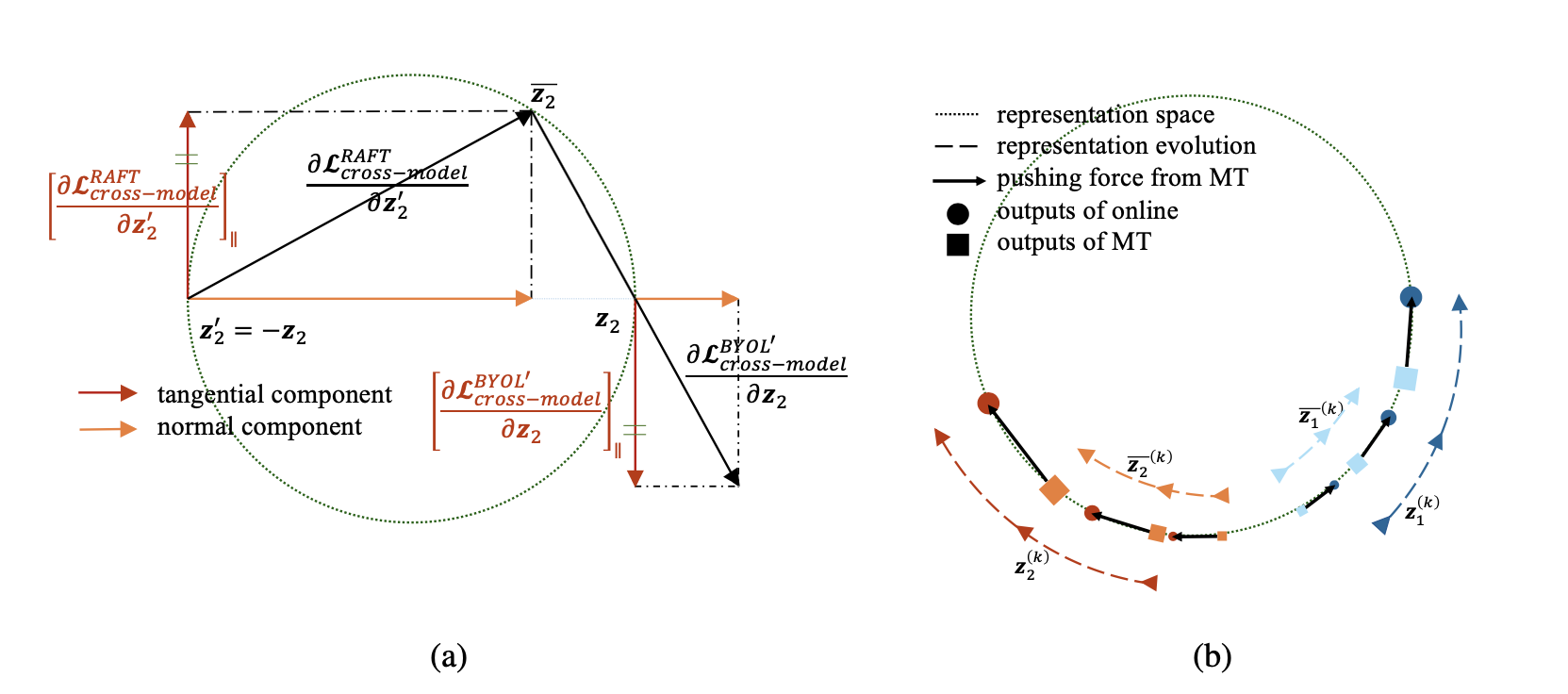
以上一一映射的建立告诉我们RAFT和BYOL$^\prime$作为representation learning framework是等价的,它们能够通过优化不同的目标得到完全一致的encoder network。这个等价性可以帮助我们解释许多关于BYOL的奇怪现象:首先因为RAFT是一个直觉上不发生collpase的方法,所以BYOL在以上条件近似成立的时候也不会发生collpase;其次是它解释了为什么我们不能够用最终的convergence来预判BYOL是否work:RAFT的正则项$-\mathcal{L}_{\text{cross-model}}$持续地让当前sample的表征远离自己过去表征的EMA,所以根本不会有convergence的出现。这一点也被BYOL工作的最新版本验证:文章中汇报了模型的非收敛性。
]]>