Introduction
之前使用的State Value或者Action-state Value均采用一一对应的方式,也就是每个状态动作对都会对应一个价值。但是随着问题的复杂化,例如当动作空间变得更多,状态集合变得更大,维持着一张Q table就不再是能够接受的事情。所以在这样的背景下,我们提出了(state-aciton/state) value function,也就是维护一组approximation weight来对当前agent所处状态和所采取动作的价值进行估计。用数学语言进行表示分别为$\widehat{V}(s ; w)$ 和 $\hat{Q}(s, a ; w)$。 使用Approximation Function的好处主要为:减少了存储空间,减少了计算量,减少了需要sample的数据(因为Approximation意味着Generalization)。
常见的function approximator有以以下:
- Linear combinations of features
- Neural networks
- Decision treees
- Nearest neighbors
- Fourier / wavelet bases
Value Function Approximation
With an Oracle
假设我们现在能够通过一个oracle访问到state value的真实值$V^{\pi}(s)$ ,那么我们对这个真实值的估计为 $\hat{V}(s ; \boldsymbol{w})$ ,对应的loss function为:
那么对应的为梯度下降值为:
利用该公式不断地去寻找local optimal即可。
Model-free VFA Policy Evaluation
当我们没有对于oracle的知识时,与之前的Model-free policy evaluation类似,为了评估当前的policy,我们需要固定住这个policy然后不断地取出sample值来估计每个state value或者state-action value。过程中我们采用的是维护一张表,但现在整个VFA的核心观点就是将这张表用一个拟合函数来代替,所以和之前有Oracle的情况类似,我们将每个sample出来的点都看作是正常值,sample的点的EV就是这个Oracle,不过会给我们的训练带来一些扰动。
我们使用一个feature vector来代表一个state $s$ 所具有的特征,那么这就是我们VFA的输入:
为了方便起见,我们使用一个线性的拟合函数来继续下面的讨论,拟合函数表示为:
同样的,损失函数的表示和上一节相同:
在MC方法中,return value是Expected Return $V^{\pi}\left(s_{t}\right)$ 无偏但是有噪声的sample,因此我们可以将MC VFA降级到一个(state, return) pair上的监督学习:
Convergence Guarantees for Linear VFA for Policy Evaluation
一个MDP当其中的Policy固定之后就是一个对应的Markov Chain,而最终会converge到一个状态分布 $d(s)$,这分布 $d(s)$ 被称作stationary distribution over states of $\pi$. 关于这个分布有以下两个性质,第一个表示所有状态的分部之和为1;第二个为一个balance equation:
定义一个关于某个特定策略下的Linear VFA的MSE为以下(relative to the true value):
Monte Carlo policy evaluation with VFA保证拟合到最小的MSE的状态:
如果是Linear的拟合函数,并且有a batch of samples,则我们能够算出weight的解析解,这里我们具体不做展开,放一张课程截图,方法就是求目标函数的导数并让其为0。

TD Learning with VFA
在TD方法中,同MC方法一样,我们将一系列的sample和特征向量降级成监督学习,这里的采用immediate reward + discounted value,是一个利用了马尔科夫性质的return的近似,从而是一个有偏估计:
在Linear TD(0)中,weights的增量为:
TD(0)方法保证拟合到一个constant factor下的最小MSE状态:
通常实践情况下TD方法的拟合会更加快。
Control using VFA
现在采用value function approximation来表示state-action values $\hat{Q}^{\pi}(s, a ; \boldsymbol{w}) \approx Q^{\pi}$,同样的我们的目标是用这个方程去尝试拟合Oracle的Q值。使用features来表示state和action的组合:
同样简化情况,使用Linear combination of features来表示state-action value function:
使用SGD来做weights的更新:
对于Model-free的情况来讲,因为没有办法直接访问到某个state的true value function,所以我们需要采用一个target value作为替代品。
在MC方法中,我们采用return $G_t$ 作为target value:
在SRASA方法中,我们采用TD target $r+\gamma \hat{Q}\left(s^{\prime}, a^{\prime} ; w\right)$,这条式子利用了当前的已经经过近似的值:
在Q-Learning方法中,我们采用TD target $r+\gamma \max _{a^{\prime}} \hat{Q}\left(s^{\prime}, a^{\prime} ; w\right)$ ,这条式子利用了max of 当前经过近似的值:
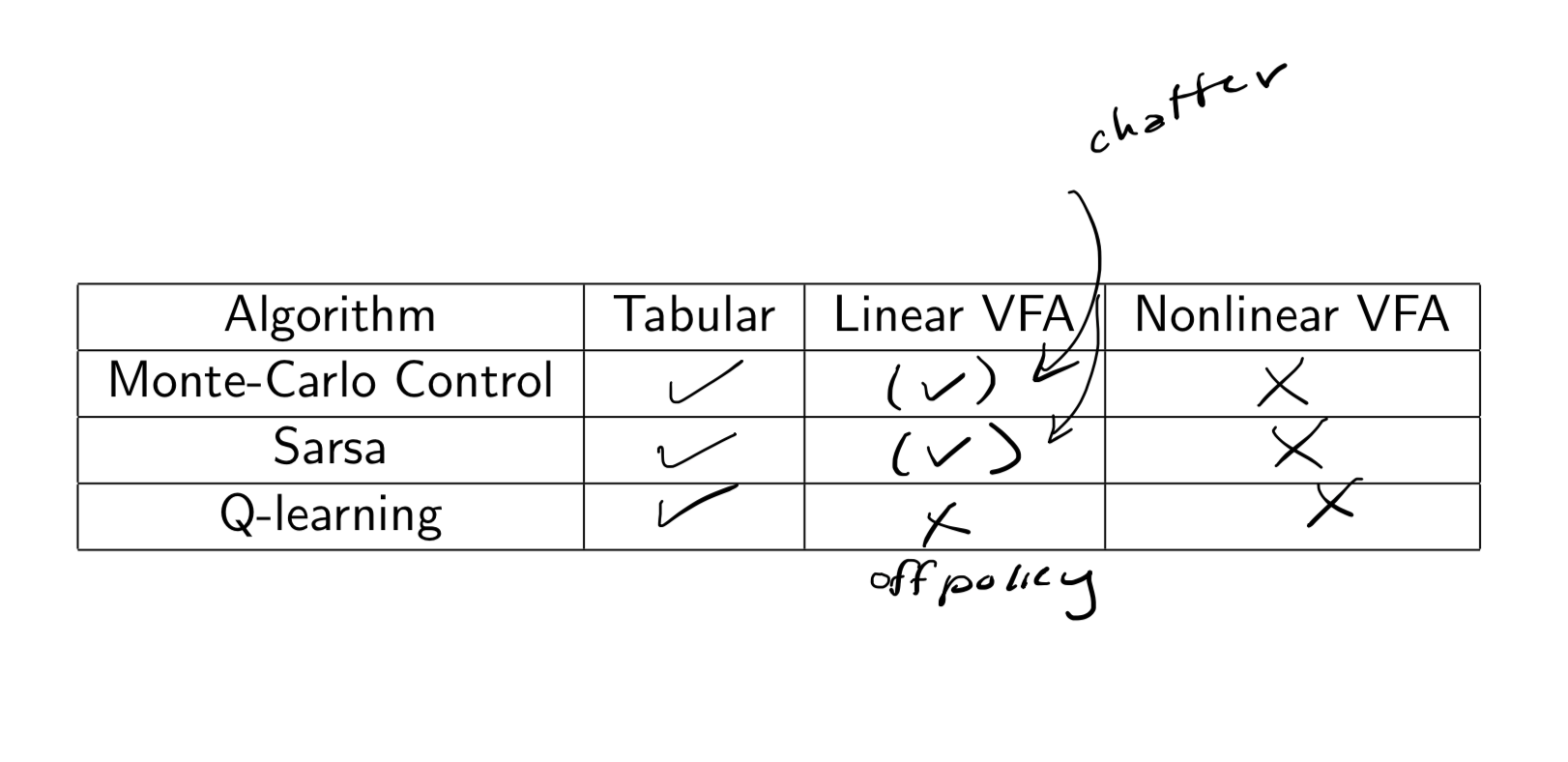
需要注意的是,TD方法中我们没有采用gradient of an objective function。关于之前VFA的Convergence的总结如下图所示,相比于算法是否拟合,更为重要的是算法最终达到的点表现如何。