Materials
- youtube demonstration on point estimation
- course note mlsc
- http://rasbt.github.io/mlxtend/user_guide/evaluate/bias_variance_decomp/
- Slides of lecture No.4 in Prof.Cai’s Machine Learning course.
- Cornel CS4780 ML course on Bias-Variance Decomposition, which explains everything!
网络上的资料覆盖了3种 bias-variance 的分解,让我在最初学习的时候有些迷惑。这篇博客依次介绍了这3种在思维复杂度上完全不同的分解推导,可以看到虽然它们都披着 Bias-Variance Decompostion 的外衣,但表述的含义是完全不同的。最为重要的是第一章节的第三section “Dataset Comes in Play”,是对这个问题最完整的分析,参考资料为Prof.Kilian Weinberger的ML课程.
Bias-Variance Decomposition
Decomposition of Point Estimation
First recall the variance definition.
Suppose that we have a point estimate $\hat \theta$ of an oracle parameter $\theta$, which is a constant vector. Substituting the “$\theta$” above with $\hat \theta - \theta$, we have:
Decomposition of EPE
We use the Expected Prediction Error (EPE) of the estimate $\hat f$ as:
The target of the machine learning is to make the EPE low. Suppose the oracle mapping from input $x$ to label $y$ is $f$ satisfying $y=f(x)$. And we have an estimate $\hat y =\hat f(x)$.
By the definition of the EPE, we can write it out in the form of $y$ and $\hat y$:
In order the extract the term of variance of $\hat y$, we add a constant term $\mathbb E(\hat y)$ into the equation, yielding:
The last term is $0$, which is easy to prove, yielding:
Dataset Comes in Play
In reality, considering the variance of the output value is not really making any sense since the problem itself might be challenging and the ground truth is of high variance. Then what does it mean when we decompose the learning objective into bias squared and variance and, oddly, where is noise? In this section, we will try to anatomize the problem of bais-variance decomposition, taking the dataset and the variance of the algorithm into account.
First let’s suppose the dataset is $D=\{(x_1,y_1), \cdots, (x_n,y_n)\}$, in which each element is independently drawn from the joint distribution: $(x,y)\sim P$. Therefore $D\sim P^n$.
Then suppose we have a learning algorithm $\mathcal A$, which takes in a dataset as an input and learns an output function $h$. We denote this function as conditioned on $D$:
We want to understand the property of the learned function $h$, not conditioned on certain dataset but the average performance of it. To achieve so, we can set the average function $\bar h$ as the expectation of $h$ over the dataset distribution:
The test error of the learner $h$ is the expected error over the training dataset $D$ and the test samples drawn independently from $P$.
Since we want to estimate the variance of the learner (how it fluctuates w.r.t its average $\bar h$), we add this term into the EPE:
The explanation of each meaningful term will be left in the following paragraphs, and before we get there let’s first eliminate $\text{term}_2$ by proving it’s $0$.
Now let’s cope with $\text{term}_1$. Denote the expectation of the true value given certain $x$ as:
The same trick applied again, we rewrite $\text{term}_1$ as:
Now we can prove that $\text{term}_3 = 0$:
Thus we have the final representation:
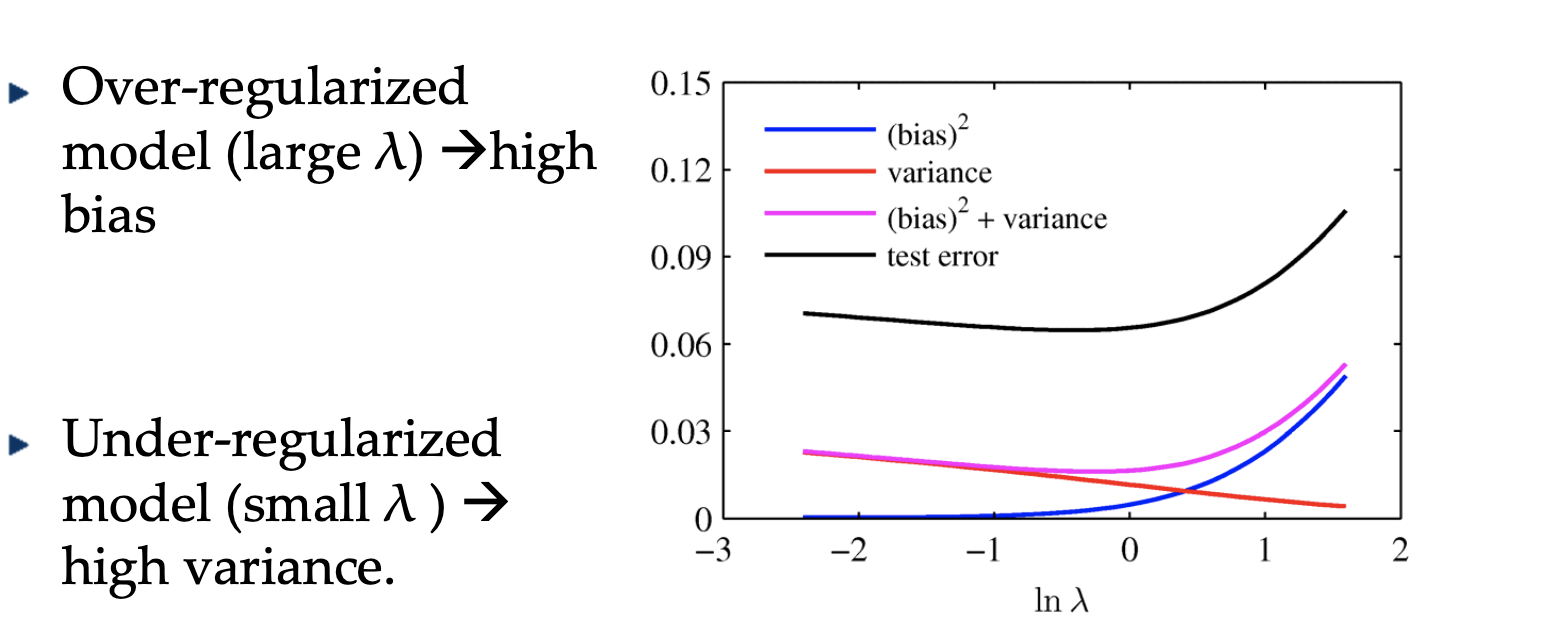
Bias-Variance Tradeoff in Regularization Method
Does it (decomposition) tell us that we cannot achieve low variance and low bias at the same time? Of course not! This target of making them both low is the whole point of the machine learning field. This decomposition helps us understand how regularization method works.
In WGAN, we learn about the K-lipschitz condition, which limits the changing speed of the the model. When using the regularization method (e.g., l1-norm and l2-norm), we are actually making the same limitation as the K-lipschitz condition (refer to the following figure).
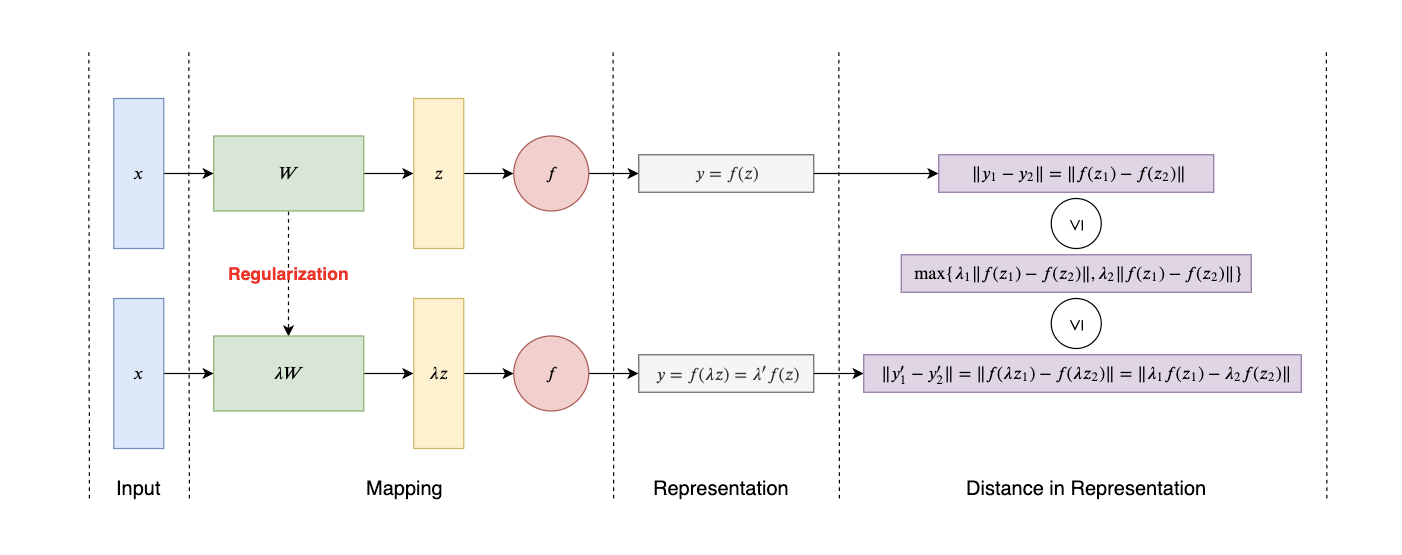
Thus the regularization method, by adding an additional loss term into the original objective, makes the output more smooth, which is equivalent to “reducing the variance of the output”. Though reducing the variance is a desirable pursuit, it cannot be achieved without sacrifice, which, in this case, is the ramification of increasing the bias of the model.
The following figure shows the tradeoff of the bias and the variance with regularization term, in which $\lambda$ represents the weight of the regularization.