Materials
Motivation
Despite the success of the Contrastive Multiview Coding (CMC), the influence of different view choices has been less studied. In this paper, we use empirical analysis to better understand the importance of view selection, and argue that we should reduce the mutual information (MI) between views while keeping task-relevant information intact. To verify this hypothesis, we devise unsupervised and semi-supervised frameworks that learn effective views by aiming to reduce their MI.
Structure of Introduction
- CMC relies on the fundamental assumption that important information is share across views, which means it’s view-invariant.
- Then which viewing conditions should it be invariant to?
- We therefore seek representations with enough invariance to be robust to inconsequential variations but not so much as to discard information required by downstream tasks.
- We investigate this question in two ways.
- Optimal choice of views depends critically on the downstream task.
- For many common ways of generating views, there is a sweet spot in terms of downstream performance where the mutual information (MI) between views is neither too high nor too low.
- InfoMin principle: A good set of views are those that share the minimal information necessary to perform well at the downstream task.
Methods
Definition 4.1. (Sufficient Encoder) The encoder $f_1$ of $v_1$ is sufficient in the contrastive learning framework if and only if $I(v_1; v_2) = I(f_1(v_1); v_2)$.
Definition 4.2. (Minimal Sufficient Encoder) A sufficient encoder $f_1$ of $v_1$ is minimal if and only if $I(f_1(v_1);v_1) \leq I(f(v_1);v_1) \forall f$, that are sufficient. Among those encoders which are sufficient, the minimal ones only extract relevant information of the contrastive task and will throw away other information.
Definition 4.3. (Optimal Representation of a Task) For a task $\mathcal T$ whose goal is to predict a semantic label $y$ from the input data $x$, the optimal representation $z^\star$ encoded from $x$ is the minimal sufficient statistic with respect to $y$. 以上说明了$z^\star$保留了所有用于和task $\mathcal T$相关的信息,因此被称作optimal的。
InfoMin Principle
作者认为good view一定是和下游任务相关联的,The following InfoMin proposition articulates which views are optimal supposing that we know the specific downstream task $\mathcal T$ in advance.

在附录中从Proposition 4.1能够推论出,遵循constraints
得到的view最优解满足以下:
在这个阶段为了说明不同view之间的information是如何影响downstream task的,文章构造了Colorful-Moving-MNIST数据集,简单来说就是带有背景的移动MNIST手写数字视频数据。
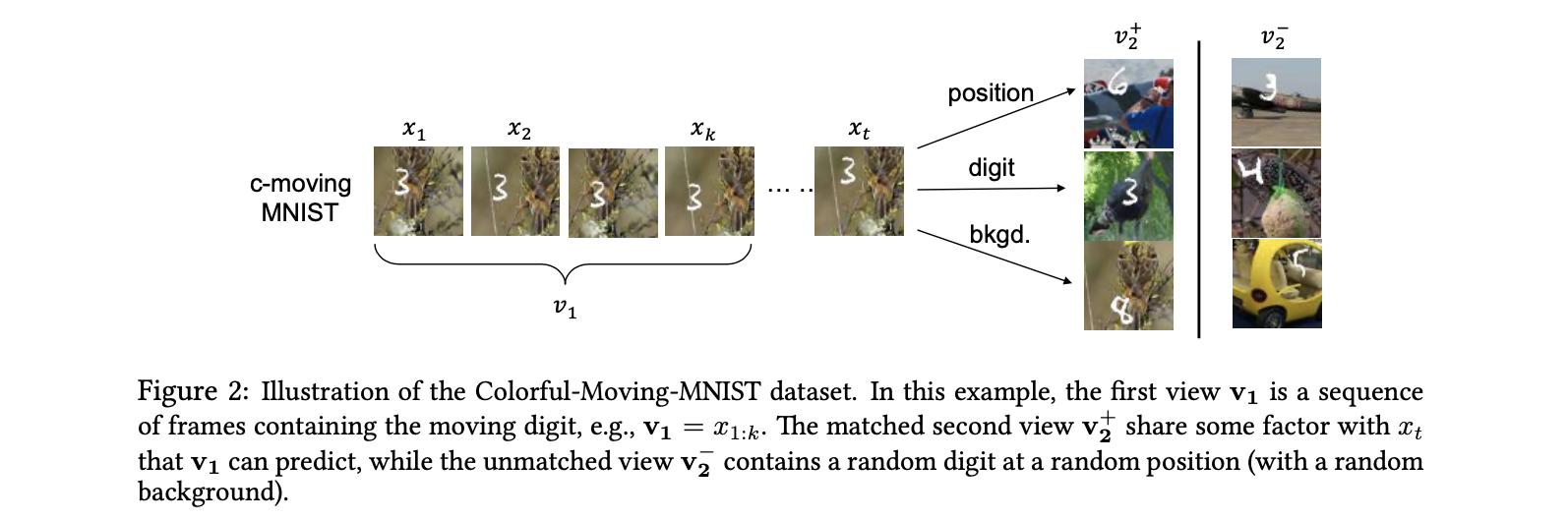
假设一个数据点是$x_{1:t}$,那么将第一个view固定为$v_1=x_{1:k}$. 在这样的设置下,因为MNIST的手写数字移动方式是固定的,所以我们可以从前2帧推知后面帧的行动,因此$I(v_1, x)$是最大化的。同时构造出三个对应不同下游任务的$v_2$,通过最大化两个view之间的MI来学到representation,最后将这个representation带入下游任务中检查其表现,得到了以下表格,证明了不同view之间分享的information将会影响representation在下游任务上的表现。

Unsupervised InfoMin
该工作实现了最小化MI的方法:那就是采用adversarial startegy解决以下的minmax problem:
这里我们复习一下GAN中adversarial training method.
