Materials
Latent Variable Models
Setting
Formally, say we have a vector of latent variables $z$ in a high-dimensional space $\mathcal Z$ which we can easily sample according to some probability density function (PDF) $P(z)$ defined over $\mathcal Z$. Then, say we have a family of deterministic functions $f (z; \theta)$, parameterized by a vector $\theta$ in some space $\Theta$, where $f:\mathcal{Z} \times \Theta \rightarrow \mathcal{X}$.
Target
We wish to optimize $\theta$ such that we can sample $z$ from $P(z)$ and, with high probability, $f (z; θ)$ will be like the $X$’s in our dataset. To make this notion precise mathematically, we are aiming maximize the probability of each $X$ in the training set under the entire generative process, according to:
In VAEs, the choice of this output distribution is often Gaussian, i.e.,
Variational Autoencoders
VAE的数学推导和Autoencoders并没有太大的关系,为什么会被叫做VAE的原因在于最后从setup推导出的training objective由encoder和decoder两个部分组成,从而成为了AE的形式。
为了最大化上文中的等式
VAE需要解决以下两个问题:(1)如何定义latent variable $z$;(2)如何处理在 $z$ 上的积分.
How to define the latent variable
第一个问题中,我们知道latent variable决定了最终数据点的形成。以手写数字数据为例,用笔的角度,起笔的位置,行笔的速度都影响最终生成的数字图像。在为这些latent variable建模的时候我们需要遵守以下另两个原则:
- Avoid deciding by hand what information each dimension of $z$ encodes
- Avoid explicitly describing the dependencies—i.e., the latent structure—between the dimensions of $z$.
在VAE中我们简单地将latent variable限制在了normal distribution上:they assume that there is no simple interpretation of the dimensions of $z$, and instead assert that samples of $z$ can be drawn from a simple distribution, i.e., $\mathcal N (0, I)$, where $I$ is the identity matrix.
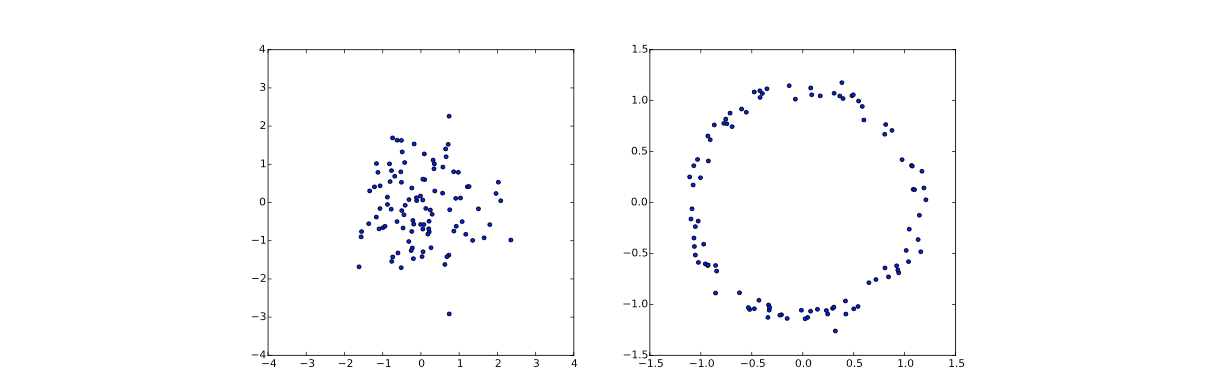
能够这么做的原因在于我们可以采用super powerful functions to map the normal distribution to some non-trivial distribution, 例如将其映射成为一个环. 我们只需要采用函数$g(z)=z/10+z/|z|$即可,下图中的左图表示从normal distribution上采样的数据点,右图则表示经过映射后的数据点分布。
1 | import numpy as np |
How to deal with the Integral
在完成以上简化后我们有$P(z)=\mathcal N(z|0, I)$. 对于一般的机器学习问题来说,我们只需要得到$P(x|z;\theta)$的公式,对其进行Monte-Carlo estimate & optimization就可以完成,但其中的问题是对于高维数据我们需要非常多的sample才能够有比较accurate estimation. 因此这不是一个tractable的方法。
Setting up the Objective
The key idea behind the variational autoencoder is to attempt to sample values of $z$ that are likely to have produced $X$, and compute $P(X)$ just from those. This means that we need a new function $Q(z|X)$ which can take a value of $X$ and give us a distribution over $z$ values that are likely to produce $X$. 这样我们在分布 $Q$ 的帮助下,就非常容易计算$E_{z \sim Q} P(X | z)$,但这只是隐变量$z$在分布$Q$下$P(X)$的估计,和真实的$P(X)$之间是有差距的,为了达到最终目的”optimize $P(X)$”,我们需要”relate $E_{z∼Q}P(X|z)$ and $P(X)$”.
这里我们选择KL divergence来描述$Q(z)$和$P(z|X)$间的差距:
使用贝叶斯条件概率公式,我们可以得到:
移项,得到:
在这条式子中,我们需要注意两点:首先,第一项$\log P(X)$对于给定的$X$来说是一个常数;第二,式子中用于将sample $X$映射到隐变量分布的$Q$是任意的分布,not just a distribution which does a good job mapping $X$ to the z’s that can produce $X$.
因为我们比较感兴趣推断$P(X)$,所以我们可以让”$Q$ depend on $X$, and in particular, one which makes $\mathcal{D}[Q(z) ||P(z | X)]$ small”.
This equation serves is the core of the variational autoencoder, and it’s worth spending some time thinking about what it says . In two sentences, the left hand side has the quantity we want to maximize: $log P(X)$ (plus an error term, which makes $Q$ produce $z$’s that can reproduce a given $X$; this term will become small if $Q$ is high-capacity). The right hand side is something we can optimize via stochastic gradient descent given the right choice of $Q$ (although it may not be obvious yet how). Note that the framework—in particular, the right hand side of the Equation—has suddenly taken a form which looks like an autoencoder, since $Q$ is “encoding” $X$ into $z$, and $P$ is “decoding” it to reconstruct $X$. We’ll explore this connection in more detail later.
总的来说,我们想要极大化左边的式子,也就是使$P(X)$能够尽量变大。同时假设如果我们有一个high-capacity $Q$,极大化左边的式子能够ideally使$Q$和$P$两者完全match. 左边的式子是没有办法直接优化的,上式给出了一个等价优化表达式,所以我们只需要关注在右式的优化即可。
Optimizing the Objective
通常我们将$Q(z|X)$限制在一个normal distribution上,即$Q(z|X)=\mathcal{N}(z | \mu(X ; \vartheta), \Sigma(X ; \vartheta))$,其中$\mu$和$\Sigma$分别为由参数$\theta$决定的deterministic function. 根据最开始我们对隐变量$z$做的假设:assert that samples of $z$ can be drawn from a simple normal distribution. 于是上式的最后一项简化成了两个multi-variant Gaussian distribution之间的KL divergence. 于是在我们的情况下,可以将该项简化成:
右式的第一项,我们可以通过在$Q$中多次采样计算平均值的方式来estimate. 从数据集$D$出发,我们重新写一下以上的优化目标式:
将优化式内部的期望拿掉,因为本来我们也就打算采用schotastic gradient descent.
There is, however, a significant problem with this equation. $E_{z∼Q} [\log P(X|z)]$ depends not just on the parameters of $P$, but also on the parameters of $Q$. However, in the equation above, this dependency has disappeared! In order to make VAEs work, it’s essential to drive $Q$ to produce codes for $X$ that $P$ can reliably decode.
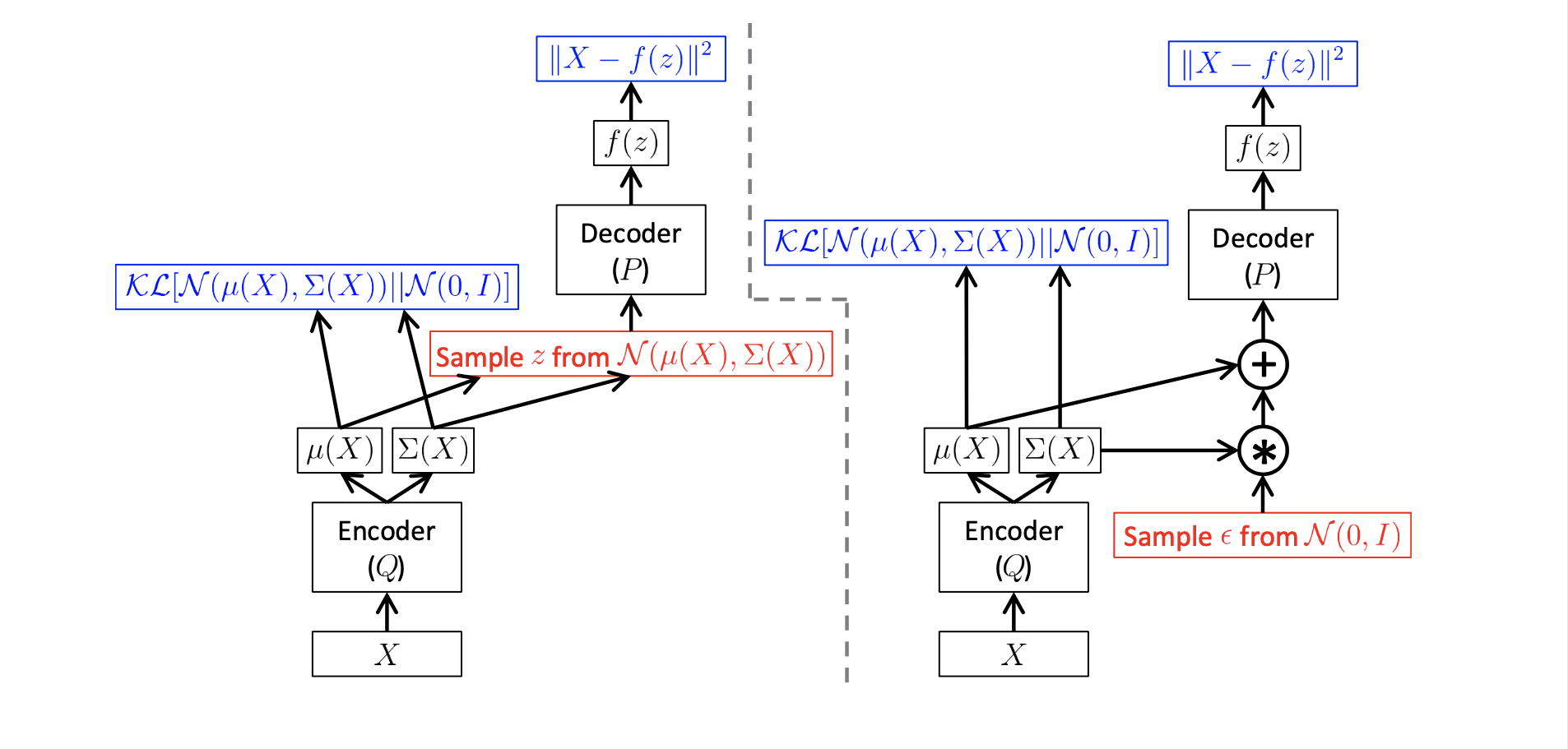
从VAE在training阶段的行为来看,因为SGD没有办法将loss传回给网络中间的sample层,所以这里VAE采用了一个reparameterization trick,具体如下图所示。